Speaker
Description
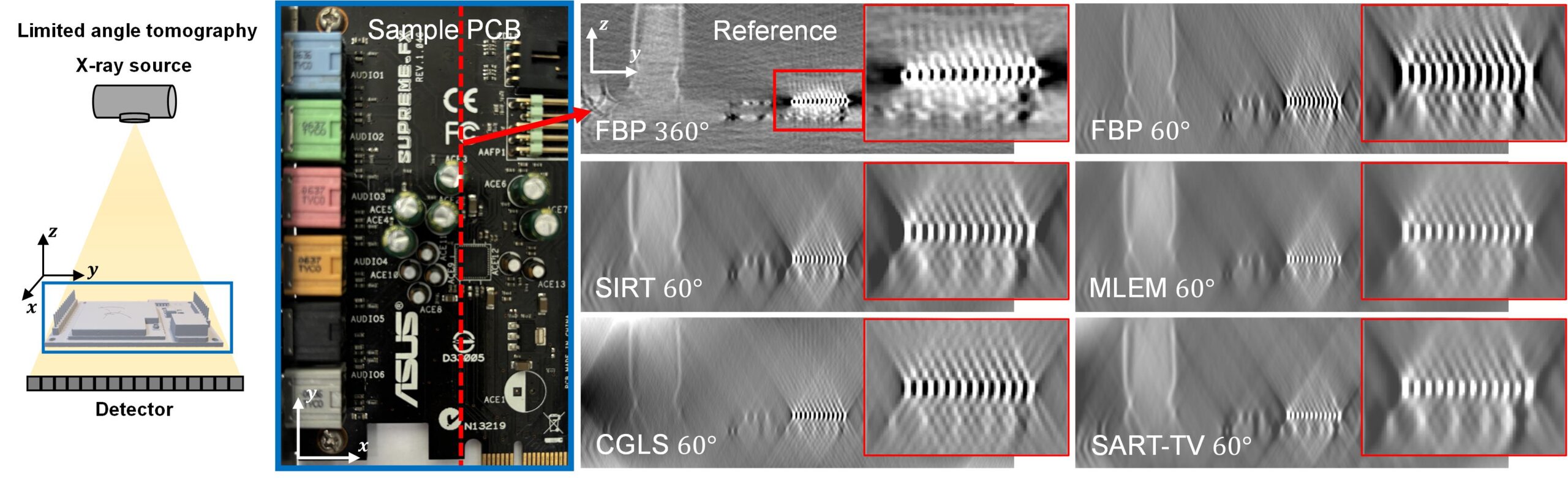
Quality assurance of many electronic parts, such as lithium-ion batteries, semiconductor packages, and multilayered printed circuit boards (PCBs), requires an exhaustive defect inspection procedure. Computed tomography may be the best non-invasive technique for identifying tiny defects inside products. Considering the geometries of the products to be investigated, the data (projections) acquisitions over 180$^{\circ}$ are sometimes unsuitable. The conventional filtered backprojection (FBP) works under the Fourier slice theorem, and the complete data-filled Fourier space guarantees the FBP-based image reconstruction. However, the limited data or angle tomography generates the null space in the Fourier domain, which causes artifacts in the reconstructed images [1]. In addition, since the FBP algorithm is based on a continuous function, which does not match the acquired projections that are discrete data, the FBP is vulnerable to noise and prone to produce artifacts.
Iterative reconstruction (IR) starts from the discretized model ($A\mathbf{x}=\mathbf{b}$) that incorporates the data ($\mathbf{b}$) that is available. Therefore, the reconstructed image ($\mathbf{x}$) is relatively robust to noise and artifacts. Moreover, IR can be applied to any scanning trajectories by properly designing $A$, which describes rays from the x-ray source through the object to the detector pixels. The recent availability of large computational capacities and their progressive improvements push the replacement of FBP by IR.
In this study, we apply various IR algorithms to the limited angle tomography of PCBs and investigate their feasibility in comparison with FBP. The investigating IR algorithms include the algebraic reconstruction technique (ART), ART with total-variation regularization, statistical reconstruction with the maximum likelihood expectation maximization (ML-EM) algorithm, and least-squares reconstruction with conjugate gradient algorithm (CGLS). Example results are shown in the figure attached to this abstract. We describe the algorithmic differences in detail and discuss their similarities and differences quantitatively.
[1] H. H. Barrett, “Limited-angle tomography for the nineties,” J. Nucl. Med. 31(10), pp. 1688–1692, 1990
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No.2021R1A2C1010161).
Corresponding author: hokyung@pusan.ac.kr