Speaker
Description
Various computationally challenging tasks in high energy physics can be formulated as quadratic unconstrained binary optimization (QUBO) or Ising problems. The problem is designed so that the ground state of the QUBO/Ising model provides the correct answer. It is a Nondeterministic Polynomial-time (NP) complete problem, and the solution candidates diverge exponentially with the problem size. Quantum annealing (QA) hardware by D-Wave is developed to solve such problems efficiently, for example. However, QA generally provides suboptimal results when handling fully connected graphs due to the limited connectivity of qubits and hardware noise. Such a trend has been consistently observed in the previous jet clustering studies. The number of available qubits also limits the problem size that quantum annealing can directly handle. These challenges could be bottlenecks for practical applications for high multiplicity problems such as track reconstruction, as the problem size will reach a sub-million to million level at the HL-LHC.
This study introduces simulated bifurcation (SB), which overcomes those challenges. SB is a novel quantum-annealing-inspired approach and predicts the Hamiltonian ground state by classically emulating the quantum adiabatic evolution of Kerr-nonlinear parametric oscillators, exhibiting bifurcation phenomena to represent the two Ising spin states. SB can update all the Ising problem spins in parallel, allowing us to achieve computational acceleration. The original version of SB, adiabatic SB (aSB), is prone to errors originating from the continuous treatment of the spins in the classical differential equations. Two variants of SB are introduced to suppress such analog errors: ballistic SB (bSB) introduces inelastic potential walls to constrain the spin within $\pm1$. Discrete SB (dSB) further discretizes spins in the mean-field term to suppress the error. We consider these two variants in our study.
Being a “quantum-inspired” but classical algorithm, it neither suffers from quantum hardware noise nor the data-size limitations that it can handle up to around a million level. In contrast to simulated annealing, SB can run in parallel and also benefits from cutting-edge computing resources such as GPUs and FPGAs. We will present its recent applications to track and jet reconstruction.
To reconstruct tracks, hits in the silicon detectors are connected, starting from doublets, i.e., segments of two silicon hits. Then, triplets, i.e., segments of three silicon hits, are created by connecting the doublets. Triplets are connected to reconstruct the final tracks, by evaluating the consistency of the triplet momenta. The following formulation of a QUBO considered in previous studies is adopted:
\begin{equation}
O(a,b,T) = \sum_{i=1}^{N} a_i T_i + \sum_{i=1}^{N} \sum_{j<i}^{N} b_{ij} T_i T_j,
\end{equation}
where $N$ is the number of triplets, $T_i$ and $T_j$ correspond to the triplets and take the value of either zero or one, $a_i$ are the bias weights used to evaluate the quality of the triplets, and $b_{ij}$ are the coefficients that quantify the compatibility of two triplets ($b_{ij}=0$ if there is no shared hit, $=1$ if there is any conflict, and $=-S_{ij}$ if two hits are shared between the triplets). The coefficients $a_i$ and $b_{ij}$ are unitless; thus, the objective QUBO function $O(a,b,T)$ gives unitless energy. The coefficients $-S_{ij}$ quantify the consistency of the two triplet momenta and the bias weights $a_i$ defines the quality of each triplet based on the transverse and longitudinal displacements
the primary vertex.
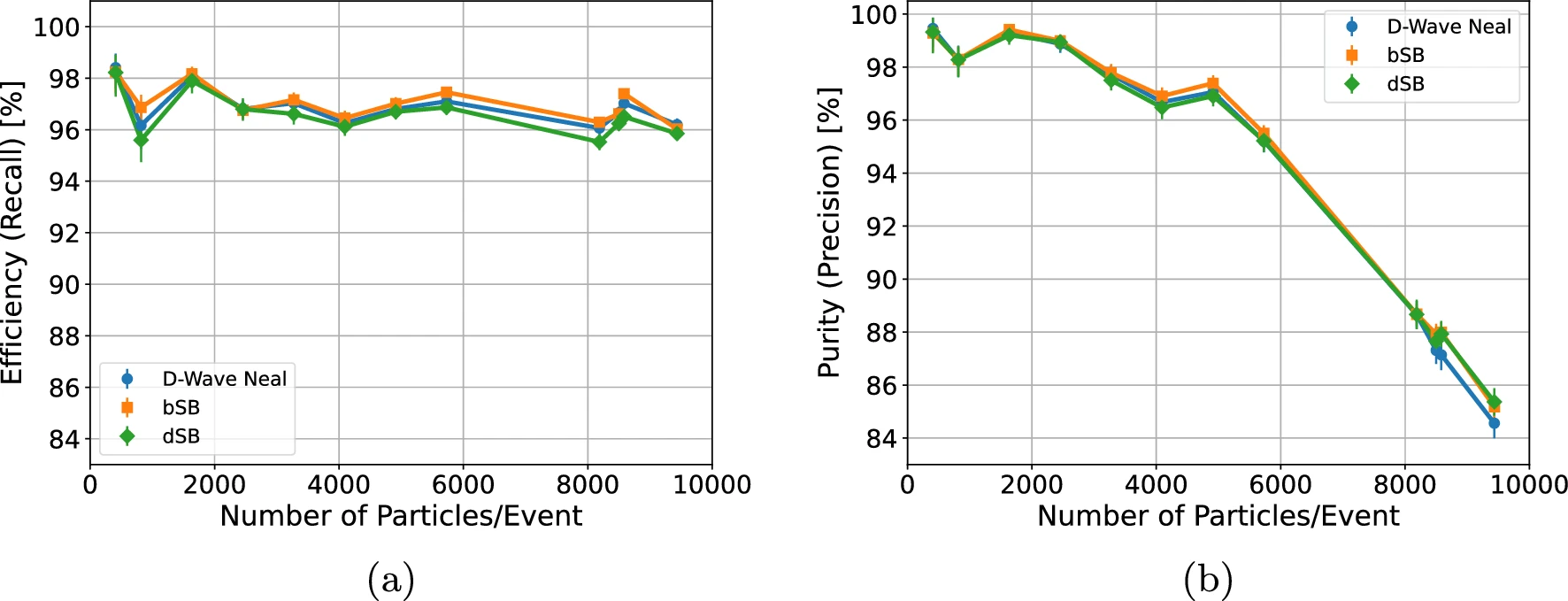
The track reconstruction performance is evaluated in terms of the efficiency and purity as presented in Figure 1. An excellent efficiency of above 95\% is obtained for all the algorithms throughout the whole dataset up to the highest particle multiplicity of approximately 10000. The purity decreases with increasing particle multiplicity but remains above 84\% for all events and above 95\% for events with a particle multiplicity of less than 6000~\cite{qaiatrack}. Finally, the execution time for each algorithm on an CPU or a GPU is evaluated (Figure 2). The impact of the GPU usage becomes significant for large-sized QUBOs, leading to a four-order-of-magnitude speed-up for the highest multiplicity event compared with D-Wave Neal simulated annealing.
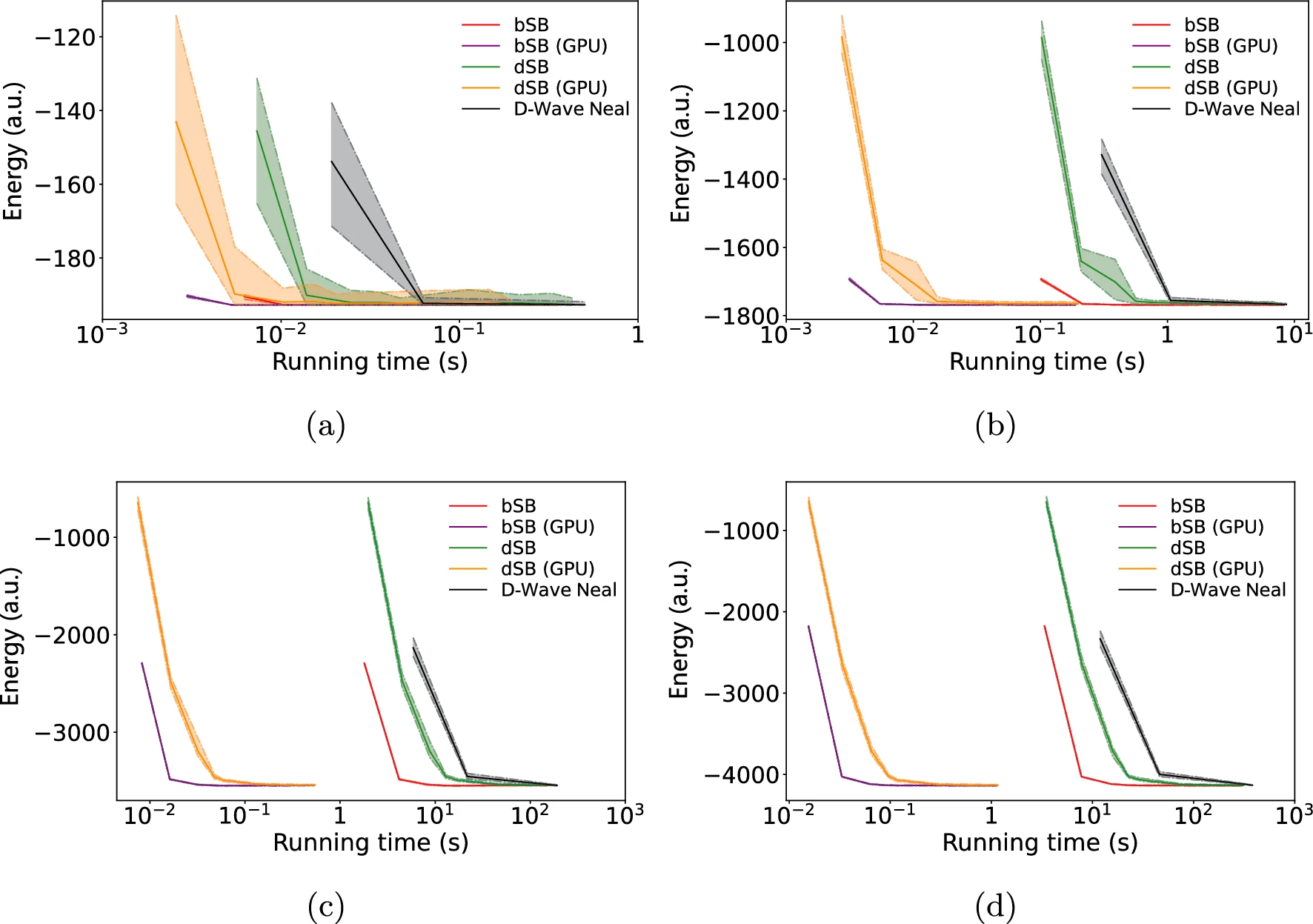
Jet reconstruction is formulated as the QUBO below~\cite{qaiajet}:
\begin{equation}
O_{\textrm{QUBO}}^{\textrm{multijet}}({s_i^{(n)}}) = \sum_{n=1}^{n_{\textrm{jet}}}
\sum_{i,j=1}^{N_{\textrm{input}}} Q_{ij} s_i^{(n)} s_j^{(n)}
+ \lambda \sum_{i=1}^{N_{\textrm{input}}}
\left( 1 - \sum_{n=1}^{n_{\textrm{jet}}} s_i^{(n)} \right)^2,
\end{equation}
where $n$ considers the jet multiplicity and the binary $s_i^{(n)}$ is defined for each $i$-th jet constituent and $n$-th jet. $Q_{ij}$ is the distance between the $i$-th and $j$-th jet constituents. In our study, we adopt the $ee$-$k_t$ distance and compare it to a simple angled-based method as a benchmark. The second term is introduced as the constraint to ensure that each jet constituent is assigned to a jet only once. This study uses Delphes fast simulated datasets for three physics processes:$e^+e^- \rightarrow Z \rightarrow q\bar{q}$, $e^+e^- \rightarrow ZH \rightarrow q\bar{q} b\bar{b}$ and $e^+e^- \rightarrow t\bar{t} \rightarrow bq\bar{q} \bar{b}\bar{q}q$. As is the case at the electron-positron colliders, the jet multiplicity is fixed to a certain value for reconstruction based on the physics process under consideration.
By using bSB and the $ee$-$k_t$ distance, we, for the first time, succeed in multijet reconstruction with a QUBO model (Figure 3), a global jet reconstruction in contrast to the traditional iterative approach. In addition, bSB also provides slightly better invariant mass resolution in $t\bar{t}$ events than FastJet (Figure 4). The results indicate that the global QUBO jet reconstruction using bSB may provide more precise jet clustering.
SB is a promising option for high energy physics due to its capability to handle large dataset at high speed and to predict ground state with outstanding performance even for fully connected QUBO problems.
References
1 H. Okawa, Q.-G. Zeng, X.-Z. Tao, M.-H. Yung, Quantum-Annealing-Inspired Algo- rithms for Track Reconstruction at High-Energy Colliders, Comput. Softw. Big Sci. 8 (1) (2024) 16. doi:10.1007/s41781-024-00126-z.
2 H. Okawa, X.-Z. Tao, Q.-G. Zeng, M.-H. Yung, Quantum-annealing-inspired algorithms for multijet clustering, arXiv:2410.14233 (2024).
Figures
Email Address of submitter
hideki.okawa@cern.ch
Short summary
Various computationally challenging tasks in high energy physics can be formulated as quadratic unconstrained binary optimization (QUBO) or Ising problems. This class of problems is designed so that the ground state of the QUBO/Ising Hamiltonian provides the correct answer. Simulated bifurcation (SB) is a novel and powerful quantum-annealing-inspired approach to solve such problems. SB predicts the ground state by classically emulating the quantum adiabatic evolution of Kerr-nonlinear parametric oscillators, exhibiting bifurcation phenomena to represent the two Ising spin states. Being a “quantum-inspired” but classical algorithm, it neither suffers from quantum hardware noise nor the data-size limitations that it can handle up to around million-level data size. In contrast to simulated annealing, SB can run in parallel and also benefits from cutting-edge computing resources such as GPUs and FPGAs. I will present its recent applications to track and jet reconstruction. For track reconstruction, we have observed as much as four orders of magnitude speedup from simulated annealing. SB is also capable of pursuing multijet reconstruction, which is formulated as fully connected QUBO problems that are notoriously known for their difficulty. SB successfully reconstruct multijet events in one go with the QUBO formulation.
[References]
• H Okawa, QG Zeng, XZ Tao, MH Yung, Springer Comput. Softw. Big Sci. 8, 16 (2024)
• H Okawa, XZ Tao, QG Zeng, MH Yung, arXiv:2410.14233 (2024)
