Speaker
Description
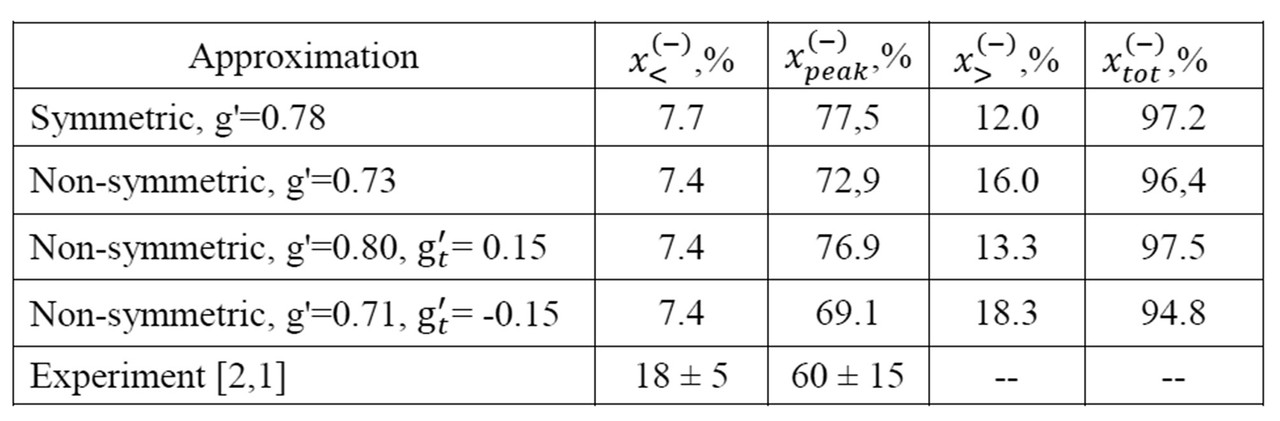
The effect is studied within a properly modified version of the continuum-random-phase-approximation (cRPA). Numerical results are obtained for the Gamow-Teller (GT) strength distribution in $^{208}Bi$. For this distribution, the experimental data concerned with the main-peak energy and the respective fraction of the Ikeda sum rule ($x_{peak}^{(-)}$) 1, and also the low-energy part distribution (total fraction $x_<^{(-)}$) [2] are available. Within the study, a realistic partially self-consistent phenomenological mean field (with parameters taken from independent data) and the spin-isovector component of Landau-Migdal forces (with the dimensionless strength g’) are exploited. In various calculations of the GT strength distribution (some results are shown in the Table), the parameter g’ is adjusted to reproduce the observed main-peak energy. There are two sources of considered tensor correlations (the latter mean a mixture of GT and respective $1^{+}$ spin-quadrupole excitations): (i) the mean-field spin-orbit term, and (ii) the appropriate component of tensor forces. Correlations of the first type are taken into account within the so-called non-symmetric version of cRPA. The corresponding equations can be found in Ref. [3]. These equations are directly extended by inclusion of the related contact tensor forces (with dimensionless strength $g_t^{'}$ ). The separable tensor forces are exploited in Ref. [4].
The calculation results obtained for various $g_t^{'}$ values (a part of results is given in the Table, where the total fraction $x_{tot}^{(-)}$ evaluated for the excitation energy interval 0-70 MeV is also shown) allow us to conclude: (i) the effect of definitely existing tensor correlations of the first type is weak; (ii) accounting for second-type correlations seems questionable and needs further consideration.
This work was supported in part by the Russian Foundation for Basic Research under grant no. 19-02-00660.
-
H. Akimune et al., Phys. Rev. C 52, 604 (1995).
-
A. Krasznahorkay et al., Phys. Rev. C 64, 067302 (2001).
-
M. G. Urin, “Relaxation of Nuclear Excitations“. Energoatomisdat, Moscow, 1991 (in Russian).
-
A. P. Severyukhin and H. Sagawa, Prog. Theor. Exp. Phys. 103D03 (2013).